Once rich control variables and fixed effects are included, researchers should assess whether serious endogeneity concerns remain. If no credible endogeneity threat can be identified, it is often preferable to rely on an efficient regression analysis with low standard errors using OLS with rich controls and fixed effects (Wooldridge 2010, p. 104). Thus, rather than immediately going down the route of instrumental variable or instrument-free approaches, we urge researchers to pause and assess how much of an endogeneity problem there may be left.
This conceptual exercise can be complemented by an empirical test for unobserved, confounding variables in the model. Importantly, treatment choice, simultaneity, measurement error, and sample selection can all be understood as special cases of omitted variable bias (Heckman 1979; Wooldridge 2010): (1) treatment choice means that the binary selection of the treatment is due to an omitted variable that determines both the treatment selection and outcome; (2) simultaneity means that the outcome affects the predictor, which can be seen as an omitted variable problem if we fail to account for the outcome, (3) measurement error means that the true variable is effectively omitted and replaced with a noisy proxy, which is mathematically similar to an omitted variable problem; and (4) sample selection means that the binary selection into the sample is due to an omitted variable that determines both the sample selection and outcome.
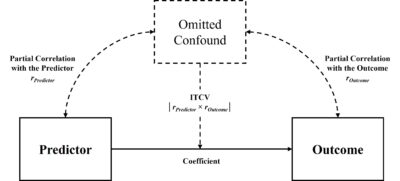
The Impact Threshold for a Confounding Variable (ITCV), developed by Frank (2000), provides a test for confounding variables. The ITCV quantifies how strong an omitted confounder’s relationship with both the predictor and the outcome would need to be—after accounting for controls and fixed effects—to nullify a statistically significant result . The ITCV therefore shifts the question from whether omitted variable bias exists to how much bias would be required to invalidate the conclusion , offering a practical benchmark for evaluating residual endogeneity risk.
References
Frank, Kenneth A. (2000), “Impact of a confounding variable on a regression coefficient,” Sociological Methods & Research, 29 (2), 147-194.
Heckman, James J. (1979), “Sample Selection Bias as a Specification Error,” Econometrica, Journal of the Econometric Society, 47 (1), 153-161.”
Wooldridge, Jeffrey M. (2010). Econometric analysis of cross section and panel data. Cambridge: MIT Press.